El valor de una acción en profundidad

Por / Publicado:
pizarra con cálculos matemáticos

Valor de una acción: ¿dónde estamos parados?

Este artículo es la continuación de la introducción que hicimos cuando explicamos de forma simplificada de qué depende el valor de una acción. En ese artículo explicamos conceptualmente lo que está detrás de la valorización de una acción.

Dado que con este sitio buscamos entregar conocimiento financiero riguroso en este artículo iremos al detalle y profundizaremos en la teoría que hay detrás del valor de una acción.

Lamentablemente ese conocimiento riguroso implica el uso de ciertas fórmulas, pero no te espantes. No son tan complejas.

Breve recapitulación

En el primer artículo de esta serie dijimos que el valor intrínseco de una acción depende de dos factores:

1. De los dividendos futuros estimados.

2. De la rentabilidad que quiere tener el mercado.

Con esos dos componentes es posible calcular el valor intrínseco de una acción. Si la acción va a pagar $110 en un año más (“estimación de dividendo futuro”), y si queremos ganar un 10% de rentabilidad (“rentabilidad que quiere el mercado”), el valor intrínseco es $100.

Pagamos $100 hoy y recibimos $110 en un año. En total ganamos $10 lo que representa una ganancia de un 10% (10/100).

Si nuestra estimación es que la compañía va a pagar $110 en 2 años (y nada más), asumiendo que queremos ganar un 10% por año, hoy estaríamos en condiciones de comprarla en $91. De esa forma nuestros $91 se convertirán en $110 en un plazo de 2 años. Y en ese caso la rentabilidad anualizada sería de un 10%.

Lo que hicimos para calcular los $100 que pagaríamos en el caso 1 y los $91 del caso 2, se llama calcular el Valor Presente. El valor intrínseco de una acción es el valor presente de sus dividendos futuros esperados, descontados a una tasa igual a la rentabilidad que el mercado quiere ganar.

Fórmula para calcular el valor presente

El valor presente de un flujo futuro se calcula con la siguiente fórmula:


Fórmula de Valor Presente

Para efectos de este artículo la tasa de descuento es la rentabilidad anual que queremos conseguir con nuestra inversión. El Flujo Futuro sería el monto que vamos a recibir en forma de dividendo. Y los períodos es la cantidad de años que tendremos que esperar para recibir ese flujo.


Si aplicas esta fórmula en los ejemplos que acabamos de revisar deberías llegar a los mismos resultados


El valor intrínseco de una acción es la suma de los valores presentes de todos los flujos futuros que generará dicha acción. Muchas veces esto implica calcular el valor presente de dividendos hasta la perpetuidad, pero por muy difícil que parezca existen metodologías matemáticas para hacer eso de forma sencilla.

Fórmula para calcular el valor presente a perpetuidad

Para calcular el valor presente de dividendos que serán pagados por una compañía hasta la perpetuidad puedes usar la siguiente fórmula:

El crecimiento anual a perpetuidad es el crecimiento que el flujo (en este caso el dividendo que paga una acción) tendrá cada año respecto al año anterior.

El valor que entrega esta fórmula corresponde al valor presente de los dividendos a perpetuidad al momento del último flujo estimado. Esto se puede observar en la siguiente imagen:

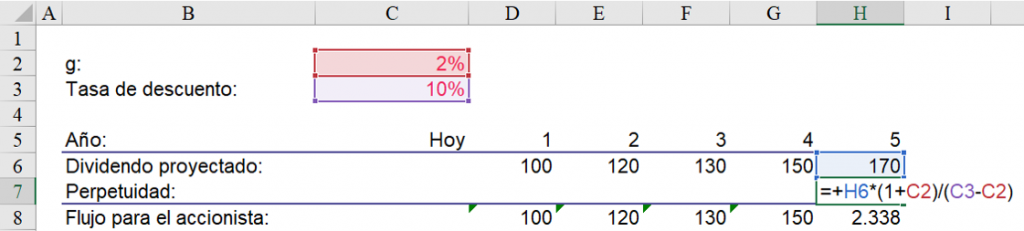
ejemplo cálculo de la perpetuidad
Cómo calcular el valor presente en Excel

Excel incluye una función que calcula automáticamente el valor presente de una serie de flujos futuros.

 

La función es =VNA(tasa de descuento ; Serie de Flujos Futuros). Si tienes Excel en inglés la función se llama =NPV.

 

Un punto a tener en consideración es que el primer flujo debe ser el flujo que ocurre en 1 año más.

 

Si por algún motivo quieres ser más detallista y considerar flujos que ocurran a mediados de cada año puedes usar la fórmula =XVNA(tasa de descuento; flujos futuros; fechas de cada flujo), donde además de los flujos debes especificar la fecha en que ocurre cada uno de esos flujos. Si tienes Excel en inglés la fórmula es =XNPV.

 

A diferencia de =VNA, la fórmula =XVNA entrega el valor presente al momento del primer flujo.

 

A modo de ejemplo, en la siguiente imagen estamos calculando el valor presente de flujos futuros en Excel asumiendo una tasa de descuento de 10%, y asumiendo que desde el año 6 hasta la perpetuidad los dividendos futuros no tienen crecimiento (es decir, asumiendo que el dividendo desde el año 6 hacia adelante es de $170):

 

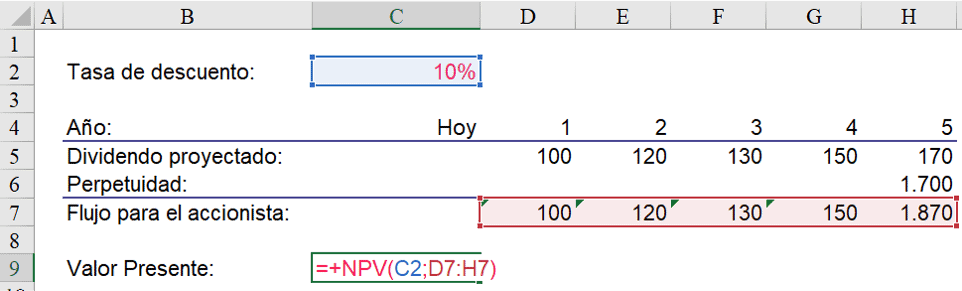
ejemplo valorización de empresa en excel

En este ejemplo, el valor presente es $1.551. Dado que en el cálculo de este valor presente exigimos una rentabilidad de un 10% anual (tasa de descuento de 10%), si calculamos la rentabilidad de un inversionista que compra la acción por $1.551 y la mantiene para siempre debería ser de un 10% anual. Si no da un 10% quiere decir que hay un error en alguna parte.

 

Una forma de hacer esta comprobación es así:

 

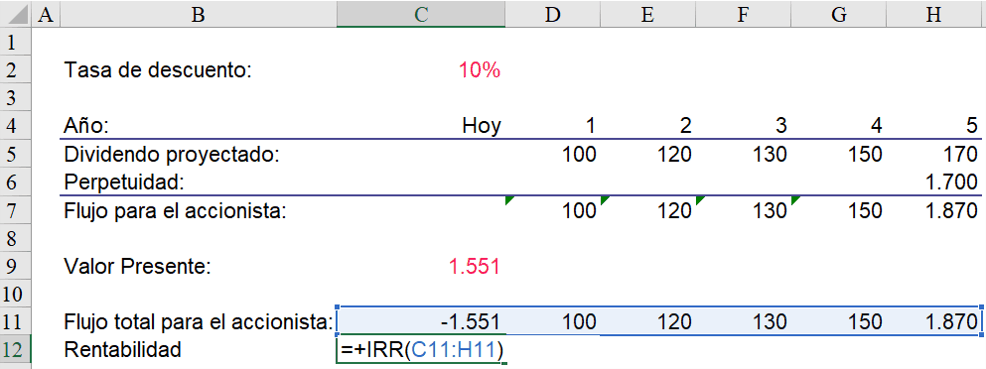
calculo de rentabilidad

En esta última imagen la fórmula =IRR calcula la Tasa Interna de Retorno, que es básicamente la rentabilidad anual del inversionista bajo ciertos supuestos que ahora no vale la pena detallar. Si tienes Excel en español la fórmula es =TIR. Si el resultado de este cálculo de la rentabilidad es distinto de la tasa de descuento que usaste en el cálculo del valor presente, entonces tienes un error en alguna parte.

¿Cuánta rentabilidad exige el mercado?

En el primer artículo de esta serie dijimos que la rentabilidad que el mercado le exige a una acción es igual a la tasa libre de riesgo más un premio por el riesgo que se toma al invertir en esa acción, y mostramos la siguiente fórmula:

costo del capital

Si bien en ese artículo comentamos algo sobre la rentabilidad libre de riesgo (o “tasa libre de riesgo”), no dijimos mucho sobre el Premio por Riesgo.

De dónde viene el premio por riesgo

Dado que se asume que un inversionista racional es averso al riesgo (por mucho que según las finanzas conductuales en algunas situaciones pueda ser risk seeker ), necesitará un premio para que esté dispuesto a invertir en activos riesgosos.

Si no tiene ningún premio, entonces invertirá en activos libres de riesgo (como los bonos del banco central). 

Mientras mayor sea el riesgo, mayor es el premio que va a exigir para invertir en ese activo. Y este concepto es el que está detrás de la fórmula que mostramos arriba.

Riesgo sistemático vs riesgo diversificable

Un inversionista racional usaría la diversificación para reducir su riesgo. Sin embargo, va a llegar un punto en que ya no pueda diversificar más (por ejemplo si invirtió en todas las acciones del mercado).

El riesgo que ese inversionista logró destruir a través de la diversificación se denomina Riesgo Diversificable, o Riesgo No Sistemático.

Y el riesgo que le queda al inversionista luego de haber diversificado al máximo su portafolio se llama Riesgo Sistemático, Riesgo No Diversificable, o Riesgo de Mercado.

Dado que hay parte del riesgo que se puede destruir (riesgo diversificable), el mercado solo exige una rentabilidad adicional por el riesgo que no puede ser eliminado.

William Sharpe - un premio nobel

Tomando esos conceptos de riesgos, William Sharpe diseñó un sistema para definir el premio por riesgo que el mercado debería exigirle a un activo en particular. Este sistema se llama Capital Asset Pricing Model (universalmente conocido como CAPM), y le valió el Premio Nobel de economía de 1990.

Este modelo dice que solo se existe un premio por el riesgo que no es diversificable (es decir, por el riesgo del mercado).

Sin embargo, hay acciones que se ven más influenciadas por el riesgo del mercado y otras que se ven menos influenciadas.

Para medir la magnitud en que el riesgo de mercado afecta a una acción en particular se usa una métrica llamada Beta.

Entendiendo el Beta de una acción

Esta métrica llamada Beta mide la magnitud en que el riesgo de mercado (riesgo sistemático) afecta a una acción en particular.

Dado que el riesgo sistemático por definición no es diversificable, mientras más expuesta esté una acción a ese riesgo, mayor será el premio que un inversionista racional le debería exigir.

El mercado tiene un Beta de 1 por definición. 

Si una acción tiene un Beta mayor que 1, significa que cuando el mercado sufre un vaivén, el valor de la acción sufrirá un vaivén de una magnitud mayor. Y una acción con un Beta menor que 1, significa que cuando el mercado sufra un vaivén el valor de la acción sufrirá in vaivén de menor magnitud.

Una acción con un Beta mayor que uno es más volátil que el mercado en general, y una acción con Beta menor que uno es una acción más defensiva. En general las compañías de servicios básicos (agua, electricidad, etc.) se asocian con un Beta menor que uno, y compañías de industrias más cíclicas, como las aerolíneas, se asocian con un Beta mayor que uno.

Un error común: Beta no es igual a Correlación

Un error muy común es asumir que el Beta de una acción es lo mismo que la correlación entre una acción y el mercado.

 

El Beta y la Correlación son cosas distintas.

 

El Beta mide cuánto se mueve el precio de una acción con los movimientos del mercado. Y la correlación mide la intensidad de la relación (lineal) entre ambas.

 

En la siguiente figura graficamos el comportamiento de dos acciones ficticias que tienen una correlación de 1,0 con el mercado (línea morada).

 

Sin embargo, una de esas acciones tiene un Beta de 0,5 (línea verde) y la otra acción tiene un Beta de 1,5 (línea rosada). Por definición, el mercado (línea morada) tiene un Beta de 1.

 

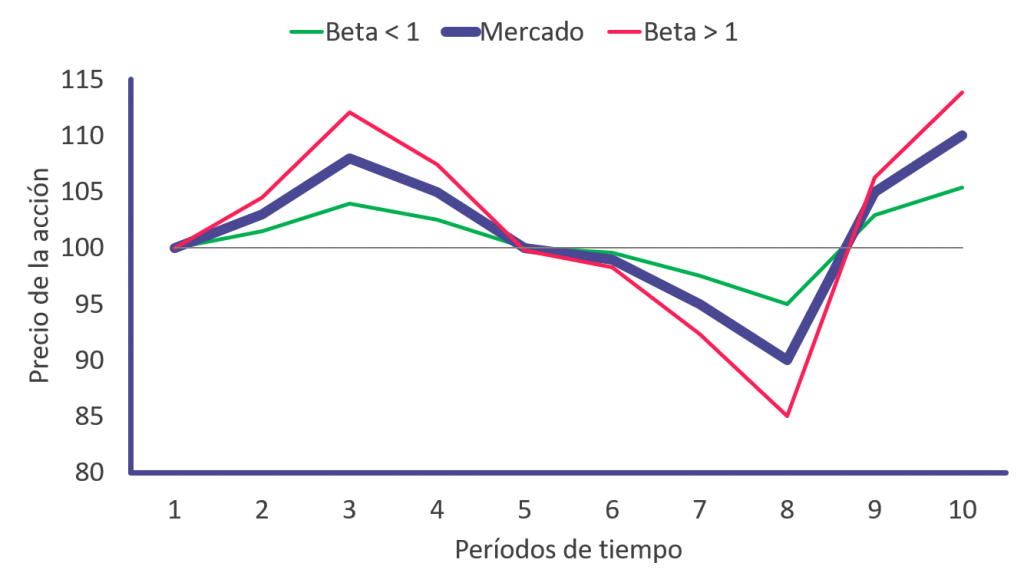
gráfico que muestra el movimiento de acciones con distinto beta pero misma correlación con el mercado

Como se puede ver, Correlación no es lo mismo que Beta.

 

También se puede ver visualmente que el Beta es una forma de medir la volatilidad de una acción en comparación con el mercado. Dicho de otra forma, el Beta es una medida del riesgo de una acción.

 

Fórmula para calcular el Beta

El Beta de una acción depende de la covarianza entre la acción y el mercado, así como también de la varianza del mercado.


La covarianza es una métrica estadística que indica en qué grado dos variables aleatorias (en este caso el retorno de una acción y el retorno del mercado) varían de forma conjunta respecto a sus medias.


Y la varianza es una métrica estadística que mide el nivel de dispersión de una variable respecto de su media.


En términos matemáticos, la fórmula del Beta es la siguiente:


Fórmula del Beta de una acción
Cómo calcular el Beta en Excel

El Beta puede calcularse fácilmente en Excel.

 

Para ello se puede usar la fórmula =PENDIENTE, o =SLOPE si tienes Excel en inglés.

 

Es importante recordar que lo que estamos calculando es cómo las variaciones del mercado afectan a la acción en particular. Por lo tanto, al calcular el Beta con la fórmula =PENDIENTE de Excel, debes asumir que el mercado es la variable del eje X (variable independiente) y que la acción es la variable del eje Y (variable dependiente).

Entendiendo el Capital Asset Pricing Model (CAPM)

Dado que según esta teoría, solo se entrega un premio por el riesgo sistemático, se puede asumir que todo el premio por riesgo depende del Beta.

En otras palabras, el premio por riesgo se calcularía de la siguiente forma:

Lo que está dentro del paréntesis es la rentabilidad que el mercado obtiene por sobre la rentabilidad libre de riesgo (dado que el mercado tiene Beta = 1, el paréntesis es igual al premio por riesgo del mercado). Es el premio recibido por el mercado para compensar por el riesgo sistemático que está tomando. Por eso se le conoce también como el premio por riesgo del mercado.

Resumiendo todo en una única fórmula, según este modelo la rentabilidad que el mercado le exige a una acción se resume así:

Fórmula de CAPM

Esto se llama Capital Asset Pricing Model (CAPM), y es la forma más utilizada en el mundo de las inversiones para calcular qué rentabilidad se le tiene que exigir a una acción. 

Según esta metodología, una acción con un Beta mayor tendería a tener un mayor retorno esperado, aunque también tendrá un riesgo mayor. Y por otro lado, una acción con un Beta menor tenderá a tener un menor retorno esperado, pero será menos riesgosa.

Conclusión

En este artículo hemos entrado en mayor profundidad en las variables que explican el valor intrínseco de una acción.

El modelo CAPM, desarrollado por el premio nobel William Sharpe, es probablemente la metodología más usada en el mundo de las inversiones para valorizar una compañía, y entrega una fórmula relativamente sencilla para estimar el retorno que el mercado le exige a una acción en particular.

CAPM asume que el único riesgo que el mercado premia es el riesgo sistemático. El riesgo no sistemático no recibiría un premio dado que un inversionista racional lo puede eliminar a través de la diversificación.

Luego, habiendo calculado la rentabilidad que se le exige a una acción, se puede calcular su valor intrínseco descontando los flujos futuros a esta tasa de descuento.

Espero que este artículo te haya ayudado a entender la teoría detrás de la valorización de una acción. En el primer artículo de esta serie explicamos de forma conceptual las variables que explican el valor de una acción.

En este segundo artículo estamos entrando en mayor detalle para aquellos que realmente quieran entender a la dinámica detrás del valor de una acción. Lamentablemente tuvimos que entrar en fórmulas y conceptos estadísticos, pero es necesario para entregar educación financiera rigurosa.

En los próximos artículos vamos a seguir profundizando en este tema y en los descubrimientos e investigaciones respecto al valor de una acción.

170 comentarios en “El valor de una acción en profundidad”

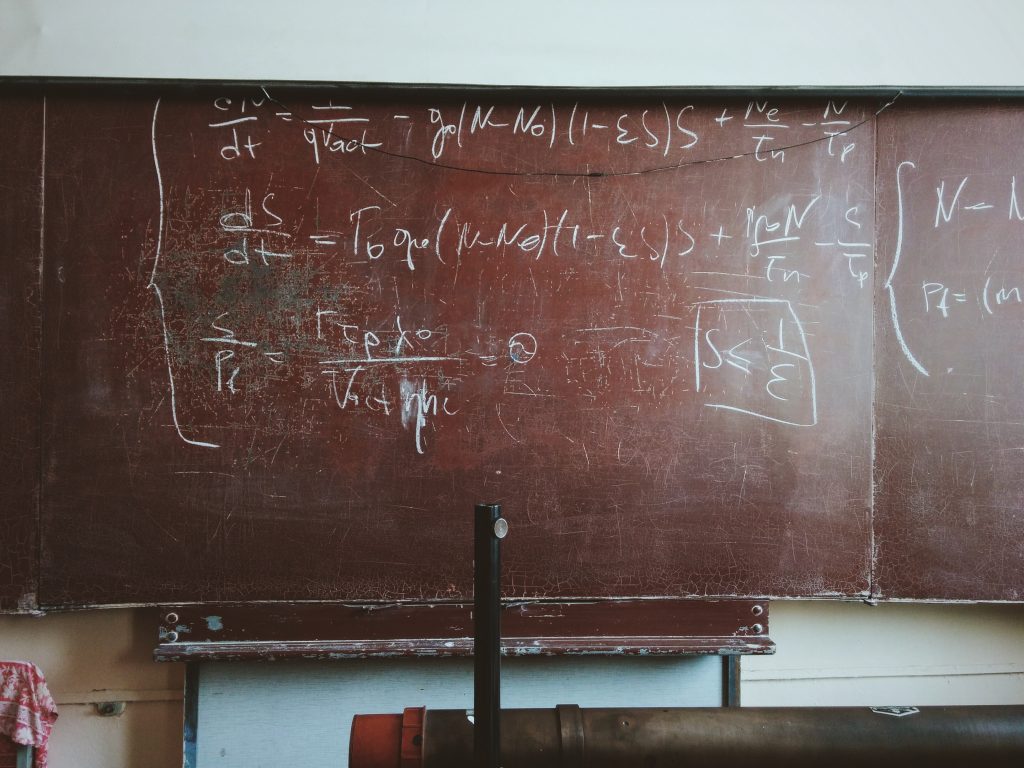
  1. Pingback: Premios Nóbel en Finanzas - Finanzas Personales

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos requeridos están marcados *