La diversificación y nuestro amigo markowitz
Un inversionista racional toma en serio la diversificación.
Si has leído nuestros artículos anteriores (por ejemplo este, también este o este de acá) ya sabrás que en inversiones siempre revisamos la relación riesgo-retorno. Los inversionistas racionales buscan maximizar su retorno y minimizar su riesgo.
El gran beneficio de la diversificación es que permite disminuir el riesgo de tu portafolio de inversiones como un todo, sin implicar necesariamente una pérdida de retorno esperado. ¿Cómo eso? Sí, disminuyes riesgo manteniendo tu retorno.
¿Suena demasiado bueno para ser verdad? Bueno, por algo a Harry Markowitz le dieron el premio nobel de economía en 1990 por su trabajo en su Teoría de Portafolio.
Este artículo está fuertemente basado en el trabajo de Markowitz.
De qué depende la rentabilidad de un portafolio
La rentabilidad esperada de un portafolio depende de la rentabilidad esperada de sus componentes. Y es simplemente el promedio ponderado.
Si inviertes la mitad de tu portafolio en un activo que tuvo un 10% de rentabilidad, y la mitad en uno que rentó un 5%, la rentabilidad de tu portafolio habrá sido un 7,5%.
Si inviertes en dos acciones distintas, pero cada una de ellas con una rentabilidad de un 10%, la rentabilidad total de tu portafolio será de un 10%.
El cálculo de la rentabilidad de un portafolio no es más complejo que eso.
De qué depende el riesgo de un portafolio
En inversiones el riesgo se suele asociar a la volatilidad. Y la volatilidad por lo general se mide con una métrica llamada desviación estándar. La desviación estándar mide qué tanto se desvía una variable respecto a su valor promedio. En el caso de las inversiones, lo que medimos es qué tanto se desvía la rentabilidad de una inversión respecto a la rentabilidad promedio.
A mayor desviación estándar, mayor volatilidad, y esto se asocia con un mayor riesgo.
El cálculo del riesgo de un portafolio es más complejo que el cálculo de la rentabilidad esperada. Si inviertes la mitad en un activo con una volatilidad de 18% y la mitad en uno de 16%, podrías terminar con una volatilidad total de un 15% (esa es la magia de la diversificación).
Y eso ocurre porque el riesgo de un portafolio no depende solo de la volatilidad de cada uno de sus componentes, sino también de la relación entre cada uno de ellos. Esa “relación” entre ellos se mide con la correlación.
La correlación mide la fuerza y dirección de la relación (lineal) entre dos variables. En español: si dos variables están muy correlacionadas, entonces tenderán a moverse juntas en la misma dirección. Si la correlación es cero entonces el movimiento de una variable no estará relacionado con el movimiento de la otra.
Y por último, si la correlación es negativa cuando una variable se mueva en un sentido la otra variable tenderá a moverse en el sentido opuesto.
Si inviertes en activos que tienden a no moverse juntos, entonces la volatilidad de uno podrá “neutralizar” parte de la volatilidad del otro.
El cálculo matemático de la volatilidad (desviación estandar) de un portafolio compuesto por dos activos es el siguiente:
Como se ve, el último término contiene un factor de correlación que hemos destacado en rosado. Si la correlación entre los dos activos es 1 entonces el resultado de la fórmula dará el promedio ponderado de las volatilidades individuales. En ese caso no existe un beneficio de la diversificación.
Sin embargo, siempre que la correlación sea menor que 1,0 la volatilidad esperada del portafolio será menor que el promedio ponderado de sus componentes. Y ahí es donde radica el beneficio de la diversificación.
Dado lo anterior, y dada la explicación matemática, siempre que la correlación entre los componentes de un portafolio sea menor que 1, el riesgo del portafolio será menor que la suma ponderada de sus partes.
Esto significa que al invertir en dos activos, el retorno que obtienes es la suma ponderada de ambas, pero el riesgo es menor que la suma ponderada de ambas. Mantienes retorno pero destruyes riesgo.
Y mientras menor sea la correlación de los activos de un portafolio mayor será la destrucción de riesgo.
Ejemplo concreto de destrucción de riesgo
Imagina que existe una acción A y una acción B. El retorno esperado de cada acción y la volatilidad de cada una de ellas se muestran en la siguiente tabla:
En este ejemplo ocurre lo siguiente:
- Si inviertes el 100% en la acción A, tu rentabilidad esperada será 10% y la volatilidad será de 18%
- Si inviertes el 100% en la acción B, tu rentabilidad esperada será 10% y la volatilidad será de 16%
- Si inviertes 50/50, tu rentabilidad esperada será de 10% y la volatilidad será de 15%
Implicancias prácticas de la diversificación
Para aplicar lo anterior en tus decisiones de inversión basta con optar por activos que estén poco correlacionados entre sí.
Una alternativa es hacer cálculos matemáticos en base a información histórica para ver como tienden a comportarse distintos activos.
Y otra alternativa es no hacer esos cálculos y usar el sentido común. Por ejemplo, las acciones de dos aerolíneas de un país probablemente tenderán a tener un comportamiento similar porque es probable que eventos que afecten a la industria afecten ambas (correlación elevada).
El comportamiento de la acción de una compañía de generación de energía probablemente será relativamente distinto al del bono que emitió un banco (correlación más baja).
En general:
- Activos que se encuentren dentro de una misma industria tenderán a tener una mayor correlación entre sí.
- Activos de un mismo país también tenderán a tener una mayor correlación entre sí.
- Activos de un mismo tipo (acciones, bonos, propiedades) también tenderán a tener una mayor correlación entre sí.
Por lo tanto, si quieres sacarle el máximo provecho a la diversificación para disminuir el riesgo de tu portafolio deberías considerar invertir en industrias distintas, geografías distintas y en tipos de activos distintos.
Frontera eficiente
Es posible hacer modelos en excel combinando no solo 2, sino cientos de activos distintos y ver los resultados en un portafolio final.
Y siguiendo esa línea, es posible hacer optimizaciones matemáticas que te entreguen el máximo retorno esperado según el nivel de riesgo que quieras.
Tranquilo, no vamos a entrar en los detalles de esos modelos matemáticos (por muy entretenido que suene) y vamos a intentar mantenernos en un nivel de profundidad suficiente para tomar mejores decisiones en tu día a día.
Bueno, volviendo a lo que estaba diciendo, es posible maximizar el retorno para el nivel de riesgo que quieras. Si uno hace esa maximización de retorno para todos los niveles de riesgos posibles llegaremos a lo que se conoce como la Frontera Eficiente. Y esto se vería así:
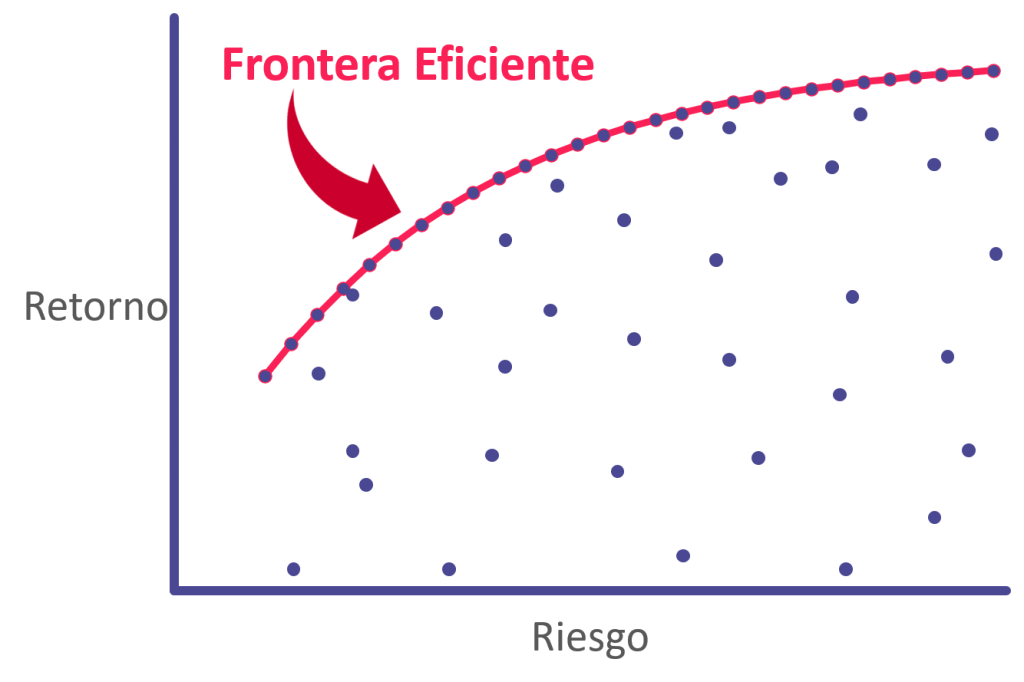
En el gráfico cada punto morado es un portafolio que se puede hacer combinando distintos activos. Cada portafolio tendrá su retorno y su riesgo esperados.
Si nos paramos en un nivel de riesgo específico, tendremos una serie de portafolios distintos, pero uno de ellos será el que entregue el mayor retorno esperado. Si dibujamos una línea entre todos los portafolios que entregan el mayor retorno esperada para cada nivel de riesgo, estaremos viendo la Frontera Eficiente.
La implicancia práctica de esto no es necesariamente comprar todos los activos que se nos pasen por delante.
Si queremos tomar un riesgo elevado para tener un retorno esperado mayor, no es necesario que invirtamos, por ejemplo, una gran parte en bonos del tesoro americano para diversificar (probablemente empujará muy para abajo el retorno esperado del portafolio). Tal vez sea conveniente invertir una parte menor en ellos, y enfocar la diversificación en acciones (renta variable) de distintas industrias y distintas regiones.
Para cada nivel de retorno esperado es posible diversificar.
Pingback: Libertad Financiera: ¡Inicio del viaje! - Finanzas Personales
Pingback: El valor de una acción en profundidad - Finanzas Personales
Pingback: Premios Nóbel en Finanzas - Finanzas Personales